A continuación, estaremos viendo el tema sobre las mediciones. Esa actividad que realizamos día a día en nuestras tareas, trabajos o en nuestras casas. La usamos para comprar una gaseosa, para decirle la hora a un amigo, o simplemente cuando tenemos que mezclar ingredientes para hacer una comida.
Por lo que en este artículo veremos la parte teórica y algunos ejemplos, y como es de costumbre al final de cada artículo educativo se dejan los links a muchos recursos didácticos, fichas y ejercicios de aplicación.
¿Qué es la medición?
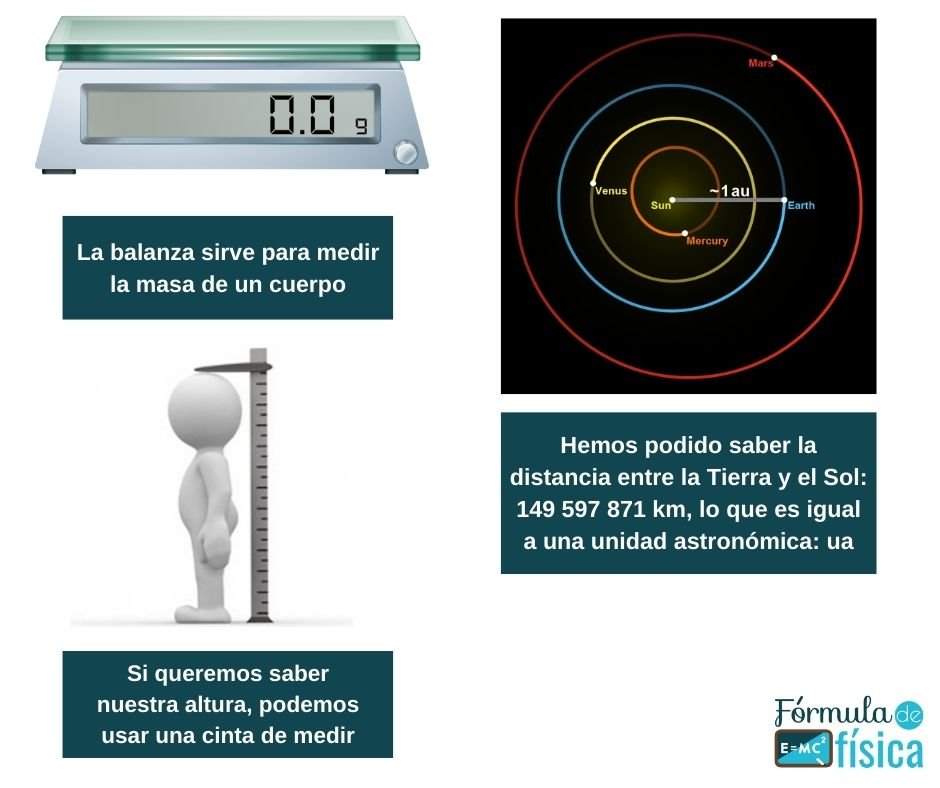
Medir es un proceso vital para la humanidad. Tal actividad viene preinstalada en nuestros cerebros esperando a que desde pequeños empecemos a desarrollarla en nuestro día a día. Así, las mediciones son importantes para conocer qué tan grande o pequeño es un objeto o fenómeno. Nos ayuda a cuantificar (dar un valor numérico) al medir la masa de un cuerpo, la distancia de la Tierra al Sol, o para saber cuál es nuestra altura en centímetros.
Al medir lo que hacemos es determinar el valor de una magnitud física. Dicho de otro modo, es comparar la magnitud física de un cuerpo (la cual se desea saber) con una unidad de medida estándar, para así estimar cuantas veces es más grande o pequeña dicha magnitud con respecto a la unidad de medida.
Entonces, conviene saber algunos conceptos:
- Una unidad de medida es una cantidad estándar de una magnitud física que después de años de estudios y experimentación se ha definido como un patrón mundial para realizar mediciones. Ejemplo: el metro y el kilogramo.
- Es importante acotar que cuando hacemos mediciones, la magnitud va acompañada de su unidad de medida. Ejemplo: 49 kg (kilogramos).
Los patrones o sistemas de medidas deben ser estandarizados. Es decir, deben poder ser reproducibles e invariantes en cualquier parte del mundo para evitar confusiones, errores. Un ejemplo de error en el uso de los sistemas de medidas fue cuando la sonda Mars Climate Orbiter se destruyó por la fricción de la atmosfera del planeta Marte.
Los científicos e ingenieros estaban empleando cálculos en el sistema inglés para enviar las señales a la sonda, y no se percataron que la misma procesaba los datos en el sistema métrico decimal. Todo esto causó que después de meses de acumular el error de navegación, finalmente la atracción de Marte terminó por atraer totalmente a la Sonda haciéndola destruirse en su atmosfera. En teoría la Sonda Mars Climate Orbite debía sobrevolar a 150 km por encima del planeta rojo; sin embargo, su altura fue de solo 57 km.

Métodos para medir
Tenemos varios métodos para medir magnitudes físicas las cuales son:
- Conteo
- Medición directa
- Medición indirecta
El proceso de conteo consiste es determinar el número de elementos de un conjunto de cosas. Al realizar este método obtendremos una medida exacta. Por ejemplo, podemos contar cinco cuadernos en un escritorio.
La medición directa consiste en comparar de manera directa (visual) la magnitud de una cantidad física con unidad de medida estándar utilizando un instrumento de medición construido para tal fin.
¿Cuáles son los instrumentos de medición directa?
A continuación verás algunos ejemplos de instrumentos de medición directa y para qué se utilizan.
- Cuando medimos la altura de una casa con una cinta métrica, procuramos observar en que número de la cinta termina el techo de la casa para así tener una medida.
- Al medir el que tiempo tarda un carro en llegar a la meta utilizando un reloj.
- La capacidad de un envase mirando la cantidad de litros (L) necesarios para llenarlo de agua (H₂O).
- Podemos usar una balanza para medir la masa de un cuerpo,
- El velocímetro de un automóvil para saber la velocidad media que lleva.
- Medir la presión arterial y saturación de oxígeno de un paciente mediante un oxímetro.
- Un odómetro (cuentakilómetros) para medir la distancia que recorre un vehículo.
La medición indirecta se basa en utilizar las mediciones directas realizadas previamente para realizar cálculos matemáticos relacionando variables para llegar al resultado. Esto surge porque que muchas veces hay magnitudes físicas que no se pueden medir por conteo o directamente con un instrumento, ya que la magnitud a medir es muy grande o muy pequeña. Entre algunas magnitudes físicas que no se pueden medir directamente son: la aceleración de un barco, la energía cinética y potencial, el área de un círculo, o el volumen de un cilindro.

Ejemplo de mediciones indirectas
- Por ejemplo, si deseamos saber el área de un círculo que tiene un radio de 5,0 metros, entonces, podemos utilizar la fórmula: A = π r2, Lo que sería: A = π (5,0 m)2 = 79 m2. Cabe resaltar que, para obtener la medida del radio, tuvimos que realizar una medición directa utilizando un instrumento que mida magnitudes física de longitud como una cinta de medir.
- Por otro lado, en caso de que no tengamos un velocímetro, podemos usar la fórmula V= d / t para medir la velocidad promedio de una moto. Para esto empleamos instrumentos de medición directa para saber la distancia recorrida y el tiempo que tarda en recorrer dicha distancia, luego efectuamos nuestro cálculo matemático y nos da la velocidad de la moto.
- Otro ejemplo sería cuando queremos saber la aceleración de la gravedad. Para eso tenemos que dejar caer un cuerpo desde una altura que hemos medido directamente con anterioridad, y como dejamos caer el cuerpo (en lugar de lanzarlo), entonces su velocidad inicial será cero, luego medir el tiempo que tarda en llegar al suelo, finalmente se emplean esos datos para determinar mediante una ecuación la aceleración de la gravedad.

Precisión y exactitud
Cuándo realizamos algún procedimiento de medición hay dos términos importantes que se deben conocer: la precisión y la exactitud; términos que son muy semejantes, pero tienen diferentes significados.
Cuando hablamos de precisión, nos referimos a que tan cerca están las mediciones realizadas entre ellas, a diferencia de la exactitud que nos muestra que tan cercano está una medida o un conjunto de mediciones del valor real. En este caso la precisión dependerá de la mínima división de la escala del instrumento. Así, un instrumento de medición es más preciso mientras más pequeño es el valor de una magnitud que puede medir; es decir, la dispersión (separación) entre las medidas es menor.
Ejemplo de algunas precisiones de medidas:
48 cm fue medido con una precisión de 1 cm
8,6 m tiene una precisión de 0,1 m
9,51 kg posee una precisión de 0,01 kg
10,205 g se midió con una precisión de 0,001 g
Cuando comparamos dos medidas y queremos saber la que tiene mayor precisión, debemos fijarnos cuál es la que tiene el menor valor. Desde luego tiene que ser representada con los mismos múltiplos y submúltiplos de la misma unidad.
Ejemplo, podemos medir con mayor precisión longitudes utilizando una regla que, con el instrumento cuentakilómetros de un automóvil. Esto debido a que la unidad mínima de la regla es el milímetro, por ende, su precisión es de ± 1 mm, mientras que la del cuentakilómetros es el kilómetro, por lo que su precisión es de ± 1 km = ± 1 000 000 mm. Ambos tienen múltiplo (km) y submúltiplo (mm) de la unidad del metro (m).

Mientras que cuando hablamos de exactitud nos a la capacidad que tiene un instrumento para proporcionar una medida muy cercana a la magnitud real. De este modo, la exactitud, es el grado de coincidencia de una medida con respecto a un valor verdadero.
Así, la exactitud depende la calidad del instrumento y de los errores sistemáticos que intervienen en el proceso de medición. Un instrumento mal calibrado nos arrojará medidas inexactas. Es importante señalar que, el valor exacto de una magnitud es algo ideal o utópico, ya que, es imposible conocerlo sin incertidumbre, por ende, siempre habrá un grado de error en la medida. Un instrumento será bastante exacto, si tiene el mínimo de errores sistemáticos presente durante la medición.

Bibliografía
Cuellar, J. (2015). Física 1. 2da edición. México. Editorial: Mc Graw Hill
Wolfgang, B & Westfall, G. (2014). Física para ingenierías y ciencias. 2da edición. México: Mc Graw Hill.








