En este nuevo artículo veremos el tema de Notación Científica y para qué nos ayudará en el campo de la física. La notación científica se puede utilizar en las medidas, operaciones matemáticas y en los datos científicos y educativos. Por eso es importante conocer esta forma de expresar los números. Es comúnmente utilizada por los químicos, biólogos, científicos, físicos, astrónomos e ingenieros. Básicamente, la notación científica significa escribir un numero comprendido entre 1 y 10 multiplicado por una potencia de base 10.
La notación científica nos ayuda a expresar números demasiado grandes o demasiados pequeños con potencias de base 10. Así, podemos manejar de forma simplificada, estandarizada y con mayor facilidad números extremadamente grandes, como la velocidad de la luz: 3×108 m/s o muy pequeños como la carga eléctrica de un electrón (e): -1,602 176 634 x 10-19 C.
Forma de la notación científica
Al escribir un número en notación científica, este queda expresado como un número mayor o igual que 1 y menor que 10 (1 ≤ B < 10). Además este número está multiplicado por una potencia de base 10 de exponente entero.

Las partes de la notación científica son:
- Mantisa: es la parte decimal, este número está comprendido entre 1 y 10
- Base: se utiliza la potencia de base 10
- Exponente: será un número entero e indica el numero de veces que la coma se mueve. Si la coma se mueve a la izquierda el exponente será positivo (+) y si se mueve a la derecha. entonces, será negativo (-).
Veamos los siguientes ejemplos:
- 3,9 x 103
- 8,1 x 1020
- 4,598 x 105
- 9,5 x 102
¿Como escribir números en notación científica?
A continuación, veremos como escribir los números en notación científica identificando los casos que se nos presentan.
Caso #1: Cuando tenemos un número mayor que 1.
- Vamos a proceder a correr la coma decimal a la izquierda hasta que quede a la derecha del primer dígito diferente a 0.
- Colocaremos la multiplicación por una potencia de base 10, que tendrá un exponente igual al número de lugres recorridos por la coma decimal.
526 = 5,26 x 102
6 987 = 6,987 x 103
1 656 498 = 1,656498 x 106
Nota: como se movió a la izquierda, el exponente es positivo.
Caso #2: El número dado es menor que 1.
- Vamos a correr la coma decimal a la derecha hasta que quede a continuación del primer dígito diferente a 0.
- Luego vamos a multiplicar por la potencia de base 10 y colocaremos en el exponente el número de veces que corrimos la coma decimal, solo que en este caso será negativo.
0,042 = 4,2 x 10-2
0,009 87 = 9,87 x 10-3
0,000 000 000 403 8 = 4,038×10-10
Nota: como se movió a la derecha, el exponente es negativo.

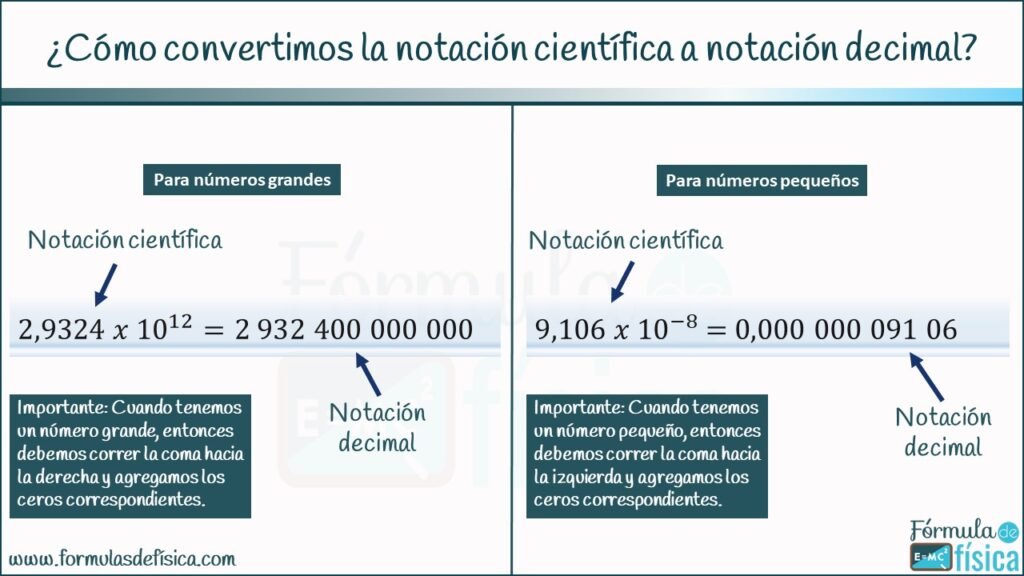
Cómo transformar de notación científica a decimal
Ahora pasaremos a aprender como transformar los números que están en notación científica a notación decimal. Es sencillo, el proceso es casi idéntico que cuando estábamos transformando de notación decimal a notación científica, a diferencia que ahora vamos a correr la coma al lado contrario. También debemos recordar que los números grandes tienen exponente positivo y los pequeños negativos.
Veamos un poco más:
- Si tenemos un número con base 10 de exponente positivo (es decir un número grande) entonces vamos a mover la coma hacia la derecha tanto lugares nos indique dicho exponente. El número quedará en su forma natural.
- Si tenemos un número con base 10 de exponente negativo (es decir un número pequeño) entonces vamos a mover la coma hacia la izquierda tanto lugares nos indique dicho exponente. El número quedará en su forma natural.
Operaciones con notación científica
También, con la notación científica podemos realizar operaciones matemáticas como: suma, resta, multiplicación y división. A continuación se expone un ejemplo por cada caso y su resolución. Para más ejercicios puedes descargarlo en el enlace que prosigue a los ejemplos.
Suma y resta de cantidades en notación científica
Cuando vamos a sumar o restar cantidades que se encuentran en notación científica debemos fijarnos si ambas tienen en sus bases de 10 potencias iguales. A continuación algunos ejemplos:
Solución: Nos fijamos que ambas bases tengan igual potencia, sacamos la base 10 como factor común. Sumamos las mantisas y luego colocamos nuestro factor común.
- Respuesta: 105 (6,2 + 2,0) = 8,2 × 105
Primer paso: Tenemos que hacer que ambas bases sean iguales, y para esto vamos a convertir uno de los dos números en potencia de base 10. En este caso vamos tomar el número: 7 × 109. Recordando que para convertir el número de notación científica a potencia de base 10, solo basta mover la coma decimal al lado que necesitemos; como necesitamos que el exponente sea 8 entonces la movemos un lugar para el lado derecho, y agregamos un cero.
- 7 × 109 = 70 × 108
Segundo paso: Ya que tenemos ambos números con las bases de exponentes iguales, podemos sacar nuestro factor común. Luego pasamos a restar las mantisas y colocamos nuestro factor común.
- 70 × 108 – 2 × 108 = 108 (70 – 2) = 68 × 108
Tercer paso: expresamos la respuesta en notación científica.
- Respuesta: 6,8 × 109
Multiplicación en la forma: Xm • Xn = Xm+n
Para multplicar bases de 10 con exponentes diferentes, colocamos la misma base y sumamos los exponentes, por ejemplo: 10m • 10n = 10m+n
Primer paso: Convertir los números a notación científica.
- 360 000 = 3,6 × 105
- 40 000 000 = 4 × 107
Segundo paso: Multiplicar las mantisas y luego las potencias de base 10 siguiendo las leyes de los exponentes.
- (3,6 × 105) (4 × 107) = 14,4 × 1012
Tercer paso: Expresar en notación científica el resultado
- Respuesta: 1,44 × 1013

División en la forma: M × 10m / N × 10n
Para dividir bases de 10 con exponentes diferentes, colocamos la misma base y restamos los exponentes, por ejemplo: 10m / 10n = 10m-n
Primer paso: Convertir los números a notación científica.
- 82 000 000 = 8,2 × 107
- 4 000 = 4 × 103
Segundo paso: Dividimos las mantisas y luego las potencias de base 10 siguiendo las leyes de los exponentes.
- (8,2 × 107) 4 × 103) = 2,05 × 104
Tercer paso: Expresar en notación científica el resultado.(No fue necesario ya que la obtuvimos directamente en la división, pero la ponemos para saber que se debe realizar en dado caso).
- Respuesta: 2,05 × 104
¿Qué números no se consideran en notación cientifica?
También es importante identificar cuando un número no está escrito en notación científica. Es por eso que lo veremos a continuación para que cuando estemos frente a los ejercicios no nos confundamos.
| 958 x 104 | No es notación científica porque la mantisa (958) es mayor que 10. El número debe estar entre 1 y 10, es decir: 1 ≤ B < 10. |
| 0,523 x 10-5 | La coma está a la izquiera del primer dígito diferente a 0. |
| 0,45 x 10-1 | Igualmente no es notación científica porque la coma decimal está a la izquierda del primer dígito diferente a 0. |
| 1,89 x 10017 | Este número no está en notación científica porque la base no es 10. Recordemos que la estructura es: mantisa x base 10n |
| 7,0 x 104,5 | No está escrito en notación científica porque el exponente de la base 10 no es un entero. |

